Ultra-compact objects
Accurate predictions of the properties of black hole mimickers, especially of their dynamics in the nonlinear regime in the case of mergers, is needed to confirm or disfavor the existence of black holes using gravitational wave or electromagnetic observations. However, for many exotic compact object models, determining their nonlinear evolution is challenging or ill-posed, due to their vastly different physical and mathematical origins. Boson stars, on the other hand, obeying standard energy conditions (as long as their potential is non-negative), evolve according to well behaved wave-like equations, and can be treated numerically using the same techniques as the Einstein equations. Thus they provide a simple and tractable setting to explore dynamical properties of ultra compact objects and black hole mimickers even in the highly dynamical non-linear regime.
Nonlinear treatment of a black hole mimicker ringdown
In this reference, we perform the first nonlinear and self-consistent study of the merger and ringdown of a black hole mimicking object with stable light rings. To that end, we numerically solve the full Einstein-Klein-Gordon equations governing the head-on collisions of a series of binary boson stars in the large-mass-ratio regime resulting in spinning horizonless remnants with stable light rings. We broadly confirm the appearance of features in the extracted gravitational waveforms expected based on perturbative methods: the signal from the prompt response of the remnants approaches that of a Kerr black hole in the large-compactness limit, and the subsequent emissions contain periodically appearing bursts akin to so-called gravitational wave echoes. However, these bursts occur at high frequencies and are sourced by perturbations of the remnant’s internal degrees of freedom. Furthermore, the emitted waveforms also contain a large-amplitude and long-lived component comparable in frequency to black hole quasi-normal modes. We further characterize the emissions, obtain basic scaling relations of relevant timescales, and compute the energy emitted in gravitational waves.
In this figure, we show (left panels) the ℓ = 2 (top) and ℓ = 8 (bottom) components of the gravitational waves emitted after the merger of the sequence of four binary boson stars compared with that of the black hole-boson star binary (labelled “Kerr”). The waveforms are aligned in time as in Figure 1. (central panels) Close-ups of the first bursts in each of the two polar modes. See Appendix B for details on uncertainties of these waveforms. (right panels) The Fourier transform of the full C = 0.38 signal as function of angular frequency ω, focusing only on dominant radiation components in each mode: the long-lived component in the ℓ = 2 mode (top) and the burst-like high-frequency component in the ℓ = 8 mode (bottom).
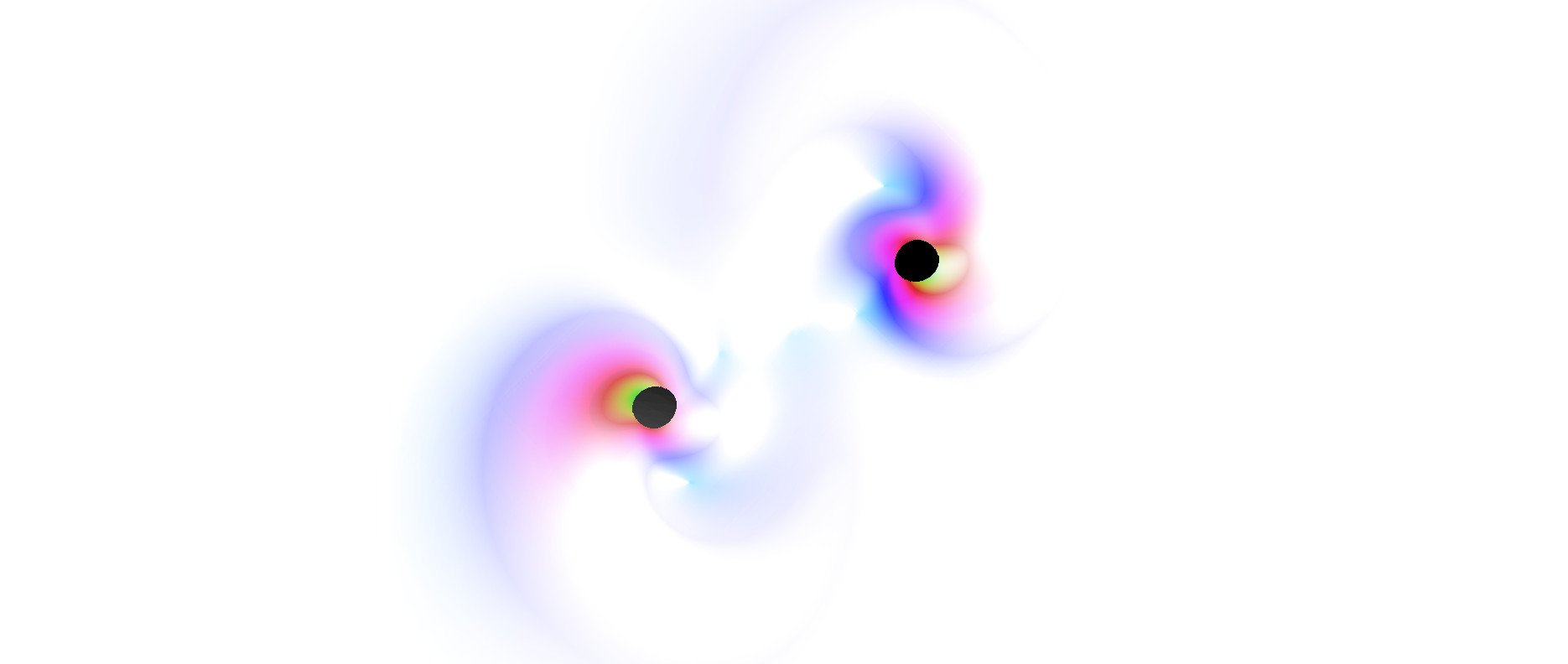
The state of the C = 0.38 binary system at selected coordinate times ˜t = (t−t0 +rextr.)/M0 during the plunge, merger, and ringdown. The main plots show the Newman-Penrose scalar Ψ4 at coordinate radii r > 3M0, which qualitatively shows the local gravitational waves. We indicate the initial production and subsequent propagation of the high-frequency component of the prompt response as “PR” together with a dotted white circle (roughly corresponding to the propagating wavefronts). Similarly, the first two gravitational wave bursts are labelled 1st and 2nd. In the region r < 3M0, we show two (black and gray) surfaces of constant scalar field magnitude |Φ| (with a close-up in the insets); recall, spinning boson stars are toroidally shaped. Arrows in the insets indicate the motion of the largest perturbation of |Φ| between snapshots. The symmetry axis is at x = 0.
Binary boson star gravitational waveforms
In this reference, we constructed constraint-satisfying initial data for a variety of binary boson star configurations. We did this using the conformal thin-sandwich formulation of the constraint equations, together with a specific choice for the matter terms appropriate for scalar fields. The free data was chosen based upon a superposition of isolated boson star solutions, but with several modifications designed to suppress the spurious oscillations in the stars that such an approach can lead to. We showed that the standard approach to reducing orbital eccentricity can be applied to construct quasi-circular binary boson star initial data, reducing the eccentricity of selected binaries to the ~ 0.001 level. Using these methods, we constructed initial data for quasi-circular binaries with different mass-ratios and spins, including a configuration where the spin is misaligned with the orbital angular momentum, and where the dimensionless spins of the boson stars exceeds the Kerr bound. We evolved these to produce the first such inspiral-merger-ringdown gravitational waveforms for constraint-satisfying binary boson stars.
Gravitational waveform of a non-spinning equal-mass eccentricity-reduced binary boson star. The movies show the corresponding binary inspiral, merger, and ring-down. Further information can be found in Fig. 8 of this reference.
Gravitational waveform of a mass-ratio 1.43 spinning eccentricity reduced binary boson star. The movies show the corresponding binary inspiral, merger, and ring-down. Further information can be found in Fig. 8 of this reference.
Formation of rotating boson stars
In this reference, we explored the nonlinear merger dynamics of binary boson stars with both non-spinning and spinning constituents. We studied the impact of interactions in the scalar matter making up these stars. In particular, we showed the pivotal role the scalar phase and vortex structure play during the late inspiral, merger, and postmerger oscillations of a binary boson star, as well as their impact on the properties of the merger remnant (see the two movies below). We demonstrated that the scalar interactions can significantly affect the inspiral gravitational wave amplitude and phase, and the length of a potential hypermassive phase shortly after merger. If a black hole is formed after merger, we found its spin angular momentum to be consistent with similar binary black hole and binary neutron star merger remnants. Furthermore, we formulated a mapping that approximately predicts the remnant properties of any given binary boson star merger. Guided by this mapping, we used numerical evolutions to explicitly demonstrate, for the first time, that rotating boson stars can form as remnants from the merger of two nonspinning boson stars. In the movie below, the merger of two non-spinning stars to a single rotating star is shown.
Movie: The evolution of the product of the phase and magnitude of the complex scalar field making up the stars in the equatorial plane of the non-spinning binary merger. For more details see Fig. 8 of this reference.
Movie: The evolution of the magnitude of the scalar field making up the boson stars inside the equatorial plane of a spinning binary throughout the merger. Due to the presence of the vortex at the center of mass of the binary, the remnant consists of two non-spinning stars (orbiting in the opposite direction as the inspiraling binary). For more information see Fig. 6 in this reference.
Stability of rotating boson stars
In this reference, I studied the stability of rotating scalar boson stars with William E. East, comparing those made from a simple massive complex scalar, to those with several different types of nonlinear interactions. We numerically evolved the nonlinear Einstein-Klein-Gordon equations in 3D, beginning with stationary boson star solutions. We showed that the linear, non-axisymmetric instability found in mini boson stars is present throughout their parameter space. However, we did find regions of parameter space where adding nonlinear interactions to the scalar potential quenches the non-axisymmetric instability, both on the non-relativistic, and the relativistic branches of solutions. For the cases exhibiting instability, we follow the nonlinear development, finding a range of dynamics including fragmentation into multiple unbound non-rotating stars, and formation of binary black holes.
Movie: The non-axisymmetric instability in a m=1 rotating boson star.
Movie: The non-axisymmetric instability in a m=2 rotating boson star.



